El procesamiento digital de imágenes es un campo de investigación abierto. El constante progreso en esta área no
ha sido por si mismo, sino en conjunto con otras áreas con las cuales esta relacionada como las matemáticas, la computación,
y el conocimiento cada vez mayor de ciertos órganos del cuerpo humano que intervienen en la percepción y
en la manipulación de las imágenes. Aunado a esto, la inquietud del hombre por imitar y usar ciertas características del
ser humano como apoyo en la solución de problemas. El avance del Procesamiento Digital de Imágenes se ve reflejado
en la medicina, la astronomía, geología, microscopía, etcétera.
Una imagen digital puede ser considerada como una matriz cuyos índices de renglón y columna
identifican un punto (un lugar en el espacio bidimensional) en la imagen y el correspondiente valor de elemento de
matriz identifica el nivel de gris en aquel punto. Los elementos de estos arreglos digitales son llamados elementos de
imagen o pixels.
En el tratamiento de imágenes se pueden distinguir tres etapas principales:
1. Adquisición de la imagen.
2. Procesamiento de la imagen.
3. Presentación al observador.
Tipos de imágenes:
 Binaria:
Binaria:
- Cada pixel es blanco o negro
- Dado que hay solo dos valores posibles 1=blanco y 0= negro, se necesita únicamente un bit por pixel.
- Tales imágenes pueden ser entonces muy eficientes en términos de almacenamiento.
- Las imágenes para las cuales la representación binaria es ideal es en el caso de texto, formas y planos arquitectónicos
Escalas de grises:
- Cada pixel es una sombra de gris
- Normalmente van de 0 (negro) a 255 (blanco) .
- Este rango indica que cada pixel puede ser representado por 8 bits o exactamente 1 byte .
- Este es un rango muy normal para manipulación de imágenes .
- Es muy común encontrarlas en imágenes de rayos x, o en imágenes de texto impreso
.jpg)
Color verdadero o RGB:
- Cada pixel tiene un color en particular, dicho color está descrito por una cantidad de rojo, una cantidad de verde y una cantidad de azul.
- Si cada uno de esos componentes tiene un rango de 0 a 255 esto da un total de 2553 = 16,777,216 diferentes colores posibles dentro de una misma imagen.
- Dado que 24 es el número total de bits para representarlos se les da también el nombre de imágenes de 24 bits.
*Para el procesamiento de imágenes en este blog utilizaremos diversas herramientas:
(Python 2.7, OpenCv 3.1.0, Numpy 1.9 & Matplolib)
Para empezar a trabajar en el procesamiento digital de una imagen es necesario, instalar el lenguaje de programación Python y un IDE ya sea Pycharm u otro de su preferencia para facilitar la comprensión de las lineas de código, así como también las librerías de complemento como: Opencv, Numpy y Matplotlib.
1.-Transformaciones Lineales en imágenes en escala de grises.
#Bibliotecas que deben exportarse para poder facilitar el código (Las que sean necesarias)
import cv2
import numpy as np
from matplotlib import pyplot as plt
#Leer una imagen: img= cv2.imread (mas la ubicacion de la imagen por ejemplo: "'C:\Python2\matt.jpg', # mas el tipo de imagen en este caso gray scale = 0")
#Mostrar la imagen= cv2.imshow
# Cerrar una ventana: cv2.destroyAllWindows()
Negativo de una Imagen
• Transformación Negativa :
s = L
– 1
–
r
• Revertiendo los niveles de
intensidad de una imagen
.
• Utilizado para mejorar
detalles blancos o grises
situados en regiones oscuras
de una imagen, cuando el área negra es dominante.
CÓDIGO PARA TRANSFORMAR UNA IMAGEN A NEGATIVO
 |
import numpy as np
import cv2
img = cv2.imread ('C:\Python2\matt.jpg',0)
row, col=img.shape
negativo=np.zeros((row,col),dtype=np.uint8)
for i in range(0,row):
for j in range (0,col):
negativo[i,j]= 255- img[i,j]
cv2.imshow ('Original',img)
cv2.imshow ('Negativo',negativo)
k=cv2. waitKey(0)
cv2.destroyAllWindows()
Transformaciones de realce de contraste
import numpy as np
from matplotlib import pyplot as plt
import cv2
img = cv2.imread ('C:\Python2\matt.jpg',0)
row, col= img.shape
minimo = np.min(img)
print minimo
maximo = np.max(img)
print maximo
contr = np.zeros( (row, col), dtype = np.uint8)
print ' en proceso...'
for i in range(0,row):
for j in range(0,col):
img2[i, j] = (img[i,j]-minimo) * 255 / (maximo-minimo)
cv2.imshow('original',img)
cv2.imshow('Contraste',contr)
k= cv2.waitKey(0)
cv2.destroyAllWindows()
Transformaciones de realce de contraste
import numpy as np from matplotlib import pyplot as plt import cv2 img = cv2.imread ('C:\Python2\matt.jpg',0) row, col= img.shape minimo = np.min(img) print minimo maximo = np.max(img) print maximo contr = np.zeros( (row, col), dtype = np.uint8) print ' en proceso...' for i in range(0,row): for j in range(0,col): img2[i, j] = (img[i,j]-minimo) * 255 / (maximo-minimo) cv2.imshow('original',img) cv2.imshow('Contraste',contr) k= cv2.waitKey(0) cv2.destroyAllWindows()
Transformación Logarítmica:
s = c log (1+r) s = c log (1+r)
c is a constante y r ≥ 0 • Usada para expandir los valores de pixeles oscuros a pixeles más claros en una imagen mientras se comprimen los valores de alto nivel.
Transformación de Potencia (Power-Law)
s = cr1/γ
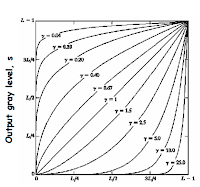 c y
γ son valores positivos y
constantes. La curva Power-law con
valores fraccionados de
γ
estrecha los valores oscuros
de entrada y amplia los niveles más claros en la salida
de la imagen
c y
γ son valores positivos y
constantes. La curva Power-law con
valores fraccionados de
γ
estrecha los valores oscuros
de entrada y amplia los niveles más claros en la salida
de la imagen
import numpy as np
import cv2
import math
img = cv2.imread('C:\Python2\his.jpg', 0)
row, col = img.shape
loga = np.zeros((row, col), dtype=np.uint8)
print ' en proceso...'
for i in range(0, row):
for j in range(0, col):
loga[i, j] = 1 * img[i, j] ** 2.0
cv2.imshow('original', img)
cv2.imshow('exponente', loga)
k = cv2.waitKey(0)
cv2.destroyAllWindows()
Transformación de Potencia (Power-Law)
s = cr1/γ
 c y
γ son valores positivos y
constantes. La curva Power-law con
valores fraccionados de
γ
estrecha los valores oscuros
de entrada y amplia los niveles más claros en la salida
de la imagen
c y
γ son valores positivos y
constantes. La curva Power-law con
valores fraccionados de
γ
estrecha los valores oscuros
de entrada y amplia los niveles más claros en la salida
de la imagen import numpy as np import cv2 import math img = cv2.imread('C:\Python2\his.jpg', 0) row, col = img.shape loga = np.zeros((row, col), dtype=np.uint8) print ' en proceso...' for i in range(0, row): for j in range(0, col): loga[i, j] = 1 * img[i, j] ** 2.0 cv2.imshow('original', img) cv2.imshow('exponente', loga) k = cv2.waitKey(0) cv2.destroyAllWindows()
Histograma
El histograma resulta muy útil para determinar si el
contraste o la exposición de una imagen digital son los adecuados.
import cv2 import numpy as np from matplotlib import pyplot as plt gray_img = cv2.imread('C:\Python2\piramide.jpg', cv2.IMREAD_GRAYSCALE) cv2.imshow('Piramide',gray_img) hist = cv2.calcHist([gray_img],[0],None,[256],[0,256]) #hist,bins = np.histogram(gray_img,256,[0,256]) plt.hist(gray_img.ravel(),256,[0,256]) plt.title('Histogram for gray scale Piramide') plt.show() print ('Valores:') print hist print ('fin') while True: k = cv2.waitKey(0) & 0xFF if k == 17: break cv2.destroyAllWindows()
Ecualización del histograma
La ecualización es un proceso similar a la normalización, en cuanto que hace más patentes las diferencias entre los distintos niveles de la imagen, añadiendo definición a esta. El proceso de ecualización modifica el histograma de tal modo que en la nueva imagen todos los niveles digitales tengan la misma frecuencia. De esta forma, se redistribuyen los valores de intensidad a lo largo de todo el espectro, igualando la presencia de estos en la imagen.
La ecualización es un proceso similar a la normalización, en cuanto que hace más patentes las diferencias entre los distintos niveles de la imagen, añadiendo definición a esta. El proceso de ecualización modifica el histograma de tal modo que en la nueva imagen todos los niveles digitales tengan la misma frecuencia. De esta forma, se redistribuyen los valores de intensidad a lo largo de todo el espectro, igualando la presencia de estos en la imagen.
import numpy as np from matplotlib import pyplot as plt import cv2 img = cv2.imread ('C:\Python2\piramide.jpg',0) equ = cv2.equalizeHist(img) res = np.hstack((img,equ)) cv2.imwrite('res.png',res) print ('en proceso...') #cv2.imshow('lion', img) cv2.imshow('resultado', res) print ('Valores:') plt.hist(equ.ravel(),256,[0,256]) plt.title('Histogram equalice for gray scale Piramid') plt.show() hist = cv2.calcHist([equ],[0],None,[256],[0,256]) while True: k = cv2.waitKey(0) & 0xFF if k == 17: break cv2.destroyAllWindows() print ('fin')
http://www.cimec.org.ar/ojs/index.php/mc/article/viewFile/3951/3868
http://docs.opencv.org/3.1.0/d5/daf/tutorial_py_histogram_equalization.html
file:///C:/Users/Diana/Downloads/Clase%20Dominio%20Espacial.pdf
http://docs.opencv.org/3.1.0/d5/daf/tutorial_py_histogram_equalization.html
file:///C:/Users/Diana/Downloads/Clase%20Dominio%20Espacial.pdf










No hay comentarios:
Publicar un comentario